排序算法整理

发表于   |   分类于 ，   |  

概况

本文简单介绍下内部排序算法的实现机制，主要包括桶排序、冒泡排序、选择排序、插入排序、快速排序、合并排序等

排序算法概述

  • 排序算法1是把列表的元素以某个顺序存放的算法，最常用的顺序是数字排序和字典顺序。有效的排序对于其它如查找和合并算法（需要输入的数据在有序的列表里）的优化使用很重要，也常常在规范化数据和生产可读输出上很有用。
  • 内部排序2：如果对象的数目足够少，可以填入到主存中，这种排序称之为内部排序
  • 外部排序：如果对象的数目足够多，以至于排序时部分对象要填入到外存中这种排序称之为外部排序

常见排序算法

桶排序

  1. 桶排序的工作流程

    先处理数组中的重复数据（有相同值的元素），然后获取数组中最大值的元素，并创建元素个数为该值的数组，接着将原数组中的每个元素依次放入新数组的指定位置（元素值等于指数值）处，最后从新数组中按顺序取出元素排序

  2. 处理重复数据

    有以下两种方式处理

    • 链表：链表的指数值为元素值，并且该数值指数处所存放的值为重复数据的个数
    • 计数器数组：采用计数的方式统计重复数据的个数，并存放在新数组的该数值指数处

  3. 实现逻辑

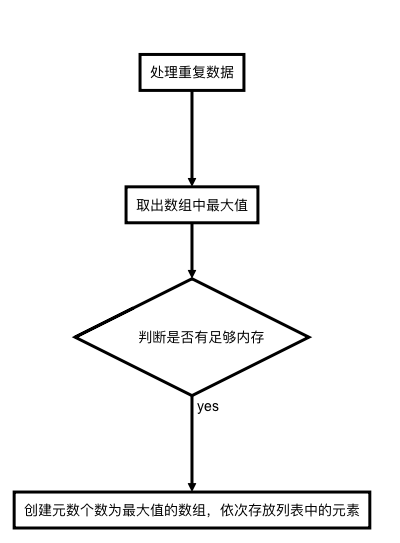
  4. 时间复杂度：O(n^2)

冒泡排序

  1. 工作流程

    通过将数组中的每个元素与它相邻的元素的值进行比较，如果不符合要求3，交换这两个元素所在位置的值，直到所有的数组元素都不能再实现交换为止。换句话说，数组中最大的元素冒出到了数组的顶端。

  2. 实现逻辑

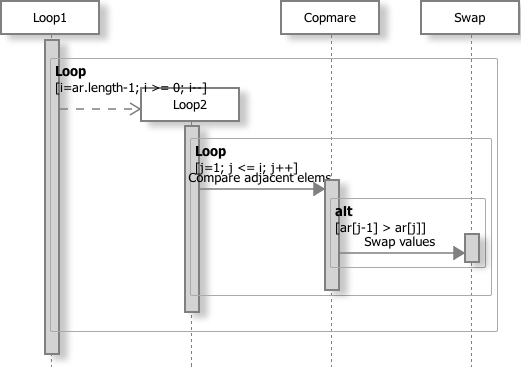
  3. 代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
     void bubbleSort(int[] ar) {
         // loop1
         for (int i = ar.length - 1; i >= 0; i--) {
           // loop2
           for (int j = 1; j <= i; j++) {
             // compare
             if (ar[j-1] > ar[j]) {
               // swap
               int temp = ar[j-1];
               ar[j-1] = ar[j];
               ar[j] = temp;
             }
           }
         }
    }

  4. 时间复杂度：[O(n), O(n^2)]

选择排序

  1. 工作流程

    选择数组中最小的未排序的条目，并移到数组的适合位置。
    遍历整个数组查找最小的元素，一旦找到，将之与数组的第一个元素交换。然后在去掉第一个元素后的数组里继续遍历查找最小的元素，依此下去。

  2. 实现逻辑

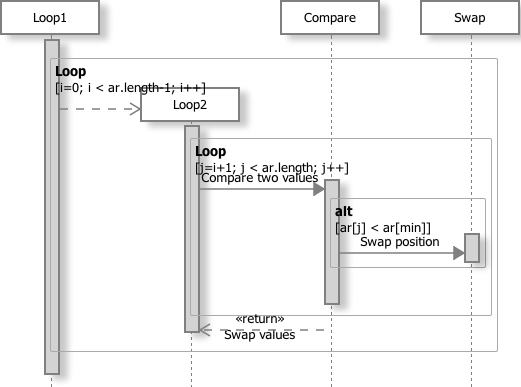
  3. 代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    void selectionSort(int[] ar) {
      // loop1
      for (int i=0; i<ar.length-1; i++) {
        int min = i;
        // loop2
        for (int j=i+1; j<ar.length; j++) {
          // compare
          if (ar[j] < ar[min])
            min = j;
        }
        // swap
        int temp = ar[i];
        ar[i] = ar[min];
        ar[min] = temp;
      }
    }

  4. 时间复杂度：[O(n), O(n^2)]

插入排序

  1. 工作流程

    每次一个条目存放进有序的数组里，直到所有的条目都已排序。

  2. 实现逻辑

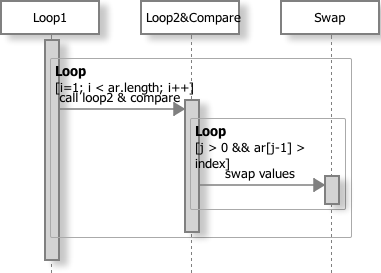
  3. 代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    void insertionSort(int[] ar) {
      // loop1
      for (int i=1; i < ar.length; i++) {
        int index = ar[i];
        int j = i;
        // loop2 & compare
        while(j > 0 && ar[j-1] > index) {
          // swap
          ar[j] = ar[j-1];
          j--;
        }
        ar[j] = index;
      }
    }

  4. 时间复杂度：[O(n), O(n^2)]

合并排序

  1. 工作流程

    基于分而治之的原则，分以下三步：

    • 把数组分割成2个或多个子数组
    • 排序每个子数组4
    • 把每个排序好的子数组合并为一个数组5

  2. 实现逻辑

  3. 时间复杂度：O(n log n)
  1. 1.Java Sorting Algorithms ↩
  2. 2.Sorting ↩
  3. 3.冒泡排序中按照从小到大的顺序依次从左到右排列 ↩
  4. 4.一般是按照从小到大的顺序排列数组的元素 ↩
  5. 5.从合并的两个数组中各取一个元素比较，取较小的数放在临时数组，直到两个数组的所有元素都放入到临时数组，即完成合并操作 ↩